Decision Trees einfach erklärt
January 31, 2021
7 min
Machine Learning
Der Decision Tree, auf Deutsch Entscheidungsbaum, ist der dritte Machine Learning Algorithmus, den wir betrachten, bevor wir uns den künstlichen neuronalen Netzen widmen. Wie bei den k-Nearest-Neighbor und Support Vector Machines auch, möchten wir hier nur eine Intuition aufzeigen, wie Decision Trees grundsätzlich funktionieren. Decision Trees werden hauptsächlich zur Klassifikation verwendet. Der Name Decision Tree leitet sich aus ihrem Erscheinungsbild ab, welches an einen Baum erinnert. Wie bei den anderen Algorithmen auch, erläutern wir die Funktionsweise eines Decision Tree an einem Beispiel. Und da regelmäßige Leser neben einem Verständnis über Machine Learning nebenbei die Grundlagen der Technik von Pumpen erlangen, bleiben wir im Bereich der Pumpen.
Grundlegender Aufbau eines Decision Tree
Der grundlegende Aufbau eines Decision Tree ist in der folgenden Abbildung dargestellt.

Ein Decision Tree wird immer von oben nach unten gelesen bzw. die Klassifikation erfolgt von oben nach unten. Für unsere Pumpe soll vorhergesagt werden, ob eine Wartung notwendig ist oder nicht. Momentan erfolgen Wartungen technischer Komponenten größtenteils nach festen zeitlichen Abständen, bspw. einmal im Jahr oder alle zwei Jahre. Dies wird als vorbeugende Instandhaltung (preventive Maintenance) bezeichnet. In unserem Beispiel soll die Wartung auf Basis des Zustandes der Komponenten erfolgen, dies wird als zustandsorientierte Instandhaltung (condition based maintenance) bezeichnet [1]. Der Vorteil dieser Instandhaltungsstrategie liegt darin, dass die Geräte dann gewartet werden, wenn es wirklich notwendig ist.
Ein Decision Tree setzt sich aus Knoten zusammen. Diese bilden die Basis für die Entscheidungen, die innerhalb eines Decision Trees getroffen werden. Der oberste Knoten wird als Wurzelknoten (Root node) bezeichnet [2]. Von dem Knoten geht eine binäre Entscheidung aus, die als Frage formuliert werden kann: Ist die Laufzeit der Pumpe größer als 2.000 Stunden? Auf diese Frage kann nur mit Ja oder Nein, also binär, geantwortet werden. Von dem Wurzelknoten gehen zwei Äste ab. Wird die Frage mit Ja beantwortet gelangen wir zu dem Knoten der fragt, ob die Pumpe Kavitation aufweist, wird die Frage mit Nein beantwortet gelangen wir zu dem Knoten der abfragt, ob die Lagertemperatur der Pumpe größer als 80 °C ist. Diese Knoten werden als innere Knoten (Internal Nodes) bezeichnet. Von diesen gehen wieder binäre Entscheidungen ab, welche die Fragen nach der Kavitation oder der Lagertemperatur der Pumpe beantworten. Die von dem Knoten der Kavitation abgehenden Äste sind beide Blattknoten (leaf nodes). Blattknoten sind die untersten Knoten innerhalb eines Decision Trees, da von ihnen keine weiteren Äste mehr abgehen. Wird die Frage nach der Kavitation mit Ja beantwortet, ist eine Wartung notwendig, bei einem Nein, ist sie nicht notwendig. Vom Knoten der Lagertemperatur gelangen wir zu einem weiteren inneren Knoten und zu einem Blattknoten. Der innere Knoten fragt nun auch nach Kavitation und so gelangen wir ebenfalls zu zwei Blattknoten. Dieses einfache Beispiel soll zunächst nur den grundsätzlichen Aufbau eines Decision Trees visualisieren. Der beschriebene Ablauf innerhalb des Decision Trees stellt den Durchlauf im Betrieb dar, also wenn für eine neue Pumpe vorhergesagt werden soll, ob sie ausfällt oder nicht. Jetzt stellt sich natürlich die Frage wie ein solcher Baum zustande kommt? Dies schauen wir uns im folgenden Abschnitt an.
Entwickeln eines Decision Tree
Wie bei den anderen Algorithmen auch benötigen wir Daten von Pumpen, um unseren Decision Tree aufbauen zu können. Die nachfolgende Tabelle stellt einen Ausschnitt von 300 fiktiven Pumpen dar. Von diesen Pumpen wurden die Parameter Laufzeit größer 2.000 Stunden, Kavitation und Lagertemperatur größer 80 °C aufgenommen und dazu aufgeschrieben, ob sie ausgefallen sind oder nicht.
Schritt für Schritt werten wir jetzt aus wie stark die einzelnen Parameter mit dem Ausfall korrelieren. Dies ist die Basis dafür, welcher Parameter den Wurzelknoten bildet. Der Wurzelknoten soll den Parameter abbilden, welcher am stärksten mit dem Ausfall korreliert. Hierzu haben wir drei kleine Decision Trees aufgezeichnet, die in der folgenden Abbildung zu sehen sind.

Jeder der Decision Trees bildet einen Parameter ab, und wie stark dieser mit dem Ausfall zusammenhängt. Betrachten wir den Parameter der Laufzeit: 140 der 300 Pumpen haben eine Laufzeit gehabt, die größer als 2.000 Stunden war, und beantworten die Entscheidungsfrage deshalb mit Ja. Von diesen 140 Pumpen sind 100 ausgefallen und 40 nicht. Von den 160 Pumpen, die weniger als 2.000 Stunden gelaufen sind, sind 39 ausgefallen und 121 nicht. Betrachten wir nun alle Parameter und wie stark diese mit dem Ausfall zusammen hängen, müssen wir feststellen, dass keiner zu 100 % mit dem Ausfall korreliert. Es kann bspw. nicht nur auf Basis der Laufzeit vorhergesagt werden, dass eine Pumpe ausfällt, da es auch Pumpen gibt, die unter 2.000 Stunden Laufzeit ausfallen und Pumpen die mit einer Laufzeit größer 2.000 Stunden nicht ausfallen. Man spricht in diesem Zusammenhang davon, dass die Daten unrein sind (impure). Der Wurzelknoten sollte immer den Parameter abbilden, welcher die niedrigste Impurity hat. Hierzu benötigen wir eine Methode, um diese Impurity zu messen. Grundsätzlich gibt es mehrere Möglichkeiten diese zu bestimmen. Eine häufig verwendete Methode stellt die Gini Impurity [3] dar, die wir im Folgenden ebenfalls verwenden.
Gini Impurity
Wir berechnen nun ausführlich die Gini Impurity für die Laufzeit, wobei wir die Berechnung auf zwei Schritte aufteilen. Zunächst berechnen wir sie einzeln für die beiden Knoten, also Laufzeit größer 2.000 Stunden gleich true und false, nach der folgenden Formel:
Ausgeschrieben bedeutet diese Formel in unserem Fall nichts anderes als:
Setzen wir unsere Zahlen für die Laufzeit ein, erhalten wir:
Je niedriger die Impurity, desto besser eignet sich der Parameter zur Vorhersage des Pumpenausfalls. Optimal wäre also eine Impurity von 0. Diese würde erreicht, wenn bei der Berechnung „Laufzeit True“ 140 der 140 Pumpen ausgefallen wären. Der schlechteste Wert, der für die Gini Impurity erreicht werden kann, ist 0,5. Dieser würde bei „Laufzeit True“ erzielt werden, wenn 70 der 140 Pumpen ausgefallen wären und 70 nicht. Wäre dies der Fall könnte der Parameter nicht zur Vorhersage verwendet werden, da er keinerlei Korrelation mit den Ausfällen aufweist, wenn 50% der Pumpen mit einer Laufzeit größer 2.000 Stunden ausfallen und 50% nicht.
Nun müssen wir die beiden errechneten Werte noch miteinander kombinieren. Für die gesamt Gini Impurity bilden wir den gewichteten Durchschnitt der beiden Blatt Impurities.
Für die Kavitation und die Lagertemperatur werden die Gini Impurities nach dem gleichen Ablauf berechnet. Für die Kavitation erhalten wir eine Impurity von 0,18, für die Lagertemperatur eine Impurity von 0,49. Die Kavitation hat demnach die mit Abstand niedrigste Impurity und korreliert am besten mit dem Ausfall. Deshalb ist der Parameter der Kavitation unser Wurzelknoten, dargestellt in der folgenden Abbildung.

Im nächsten Schritt müssen wir betrachten, ob die beiden anderen Parameter noch weitere sinnvolle Informationen liefern oder nicht. Konkret bedeutet dies, dass wir berechnen ob durch das Hinzufügen des Parameters der Laufzeit bzw. der Lagertemperatur die Impurity von 0,18 weiter reduziert werden kann. Wir setzen jetzt für jeden der inneren Knoten die entsprechenden Werte der beiden Paramater ein. Für den linken inneren Knoten sähe der weitere Verlauf wie folgt aus:
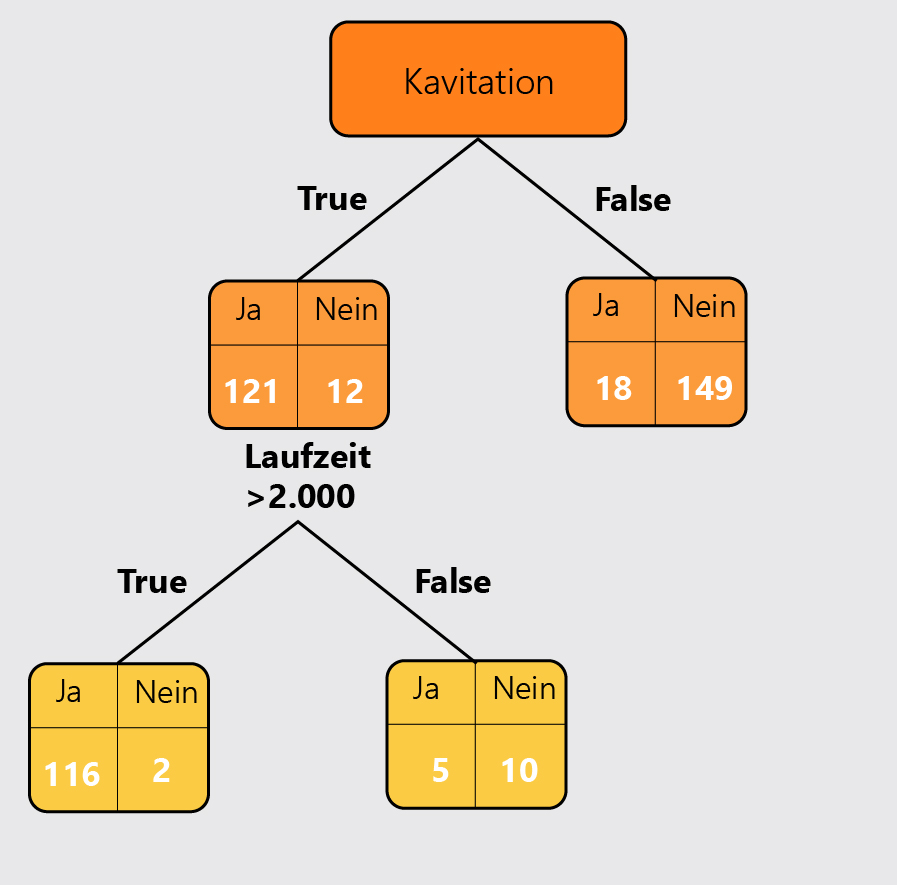
Von den 133 Pumpen mit Kavitation = True, haben 118 eine Laufzeit größer 2.000 Stunden und 15 eine Laufzeit kleiner 2.000 Stunden. Von den 118 mit der erhöhten Laufzeit sind 116 ausgefallen, von den 15 mit der niedrigen Laufzeit sind 5 ausgefallen. Wir berechnen nun die einzelnen Impurities und dann die Gesamte.
Die Impurity von 0,08 ist schon einmal ein sehr guter Wert. Nun müssen wir noch die Impurity der Lagertemperatur berechnen, um zu vergleichen welcher Parameter den besseren Wert liefert. Die Werte für den Parameter der Lagertemperatur sind in der folgenden Abbildung dargestellt.

Durch den Einsatz der Werte der Abbildung in die drei Formeln ergibt sich eine Gesamt Impuity von 0,49. Es zeigt sich, dass der Parameter der Laufzeit einen deutlich niedrigeren Wert als die Lagertemperatur liefert. Gleichzeitig zeigt die Verbesserung von 0,18 (ausschließlich Kavitation als Parameter) auf 0,08, dass der zweite Parameter einen Mehrwert liefert. Deswegen setzen wir diesen für den Knoten ein, wodurch unser Baum wie folgt aussieht.
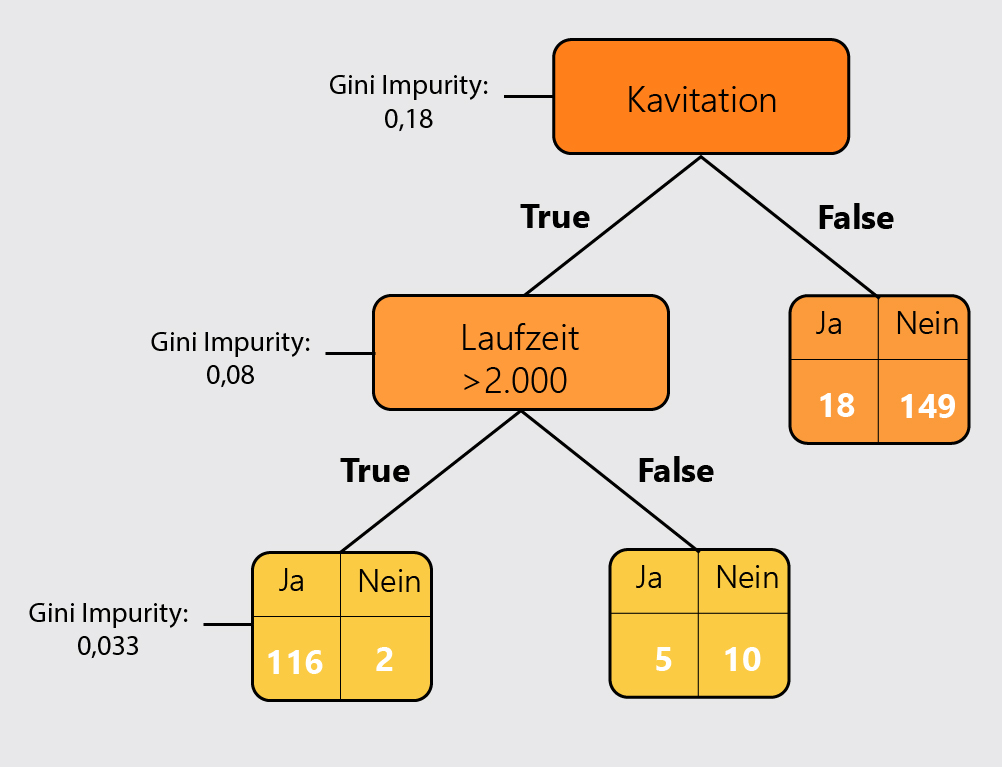
Zum Abschluss dieser Seite müssen wir noch berechnen, ob der Einsatz des letzten Parameters der Lagertemperatur eine weitere Verbesserung der Impurity liefert. Wir nehmen an, dass von den 118 Pumpen, mit einer Laufzeit größer 2.000 Stunden, 106 eine Lagertemperatur hatten die größer als 80 °C war. Von diesen sind 105 ausgefallen. Von den 12 Pumpen mit einer Temperatur kleiner 80 °C sind 10 ausgefallen und zwei nicht, dargestellt in der folgenden Abbildung.
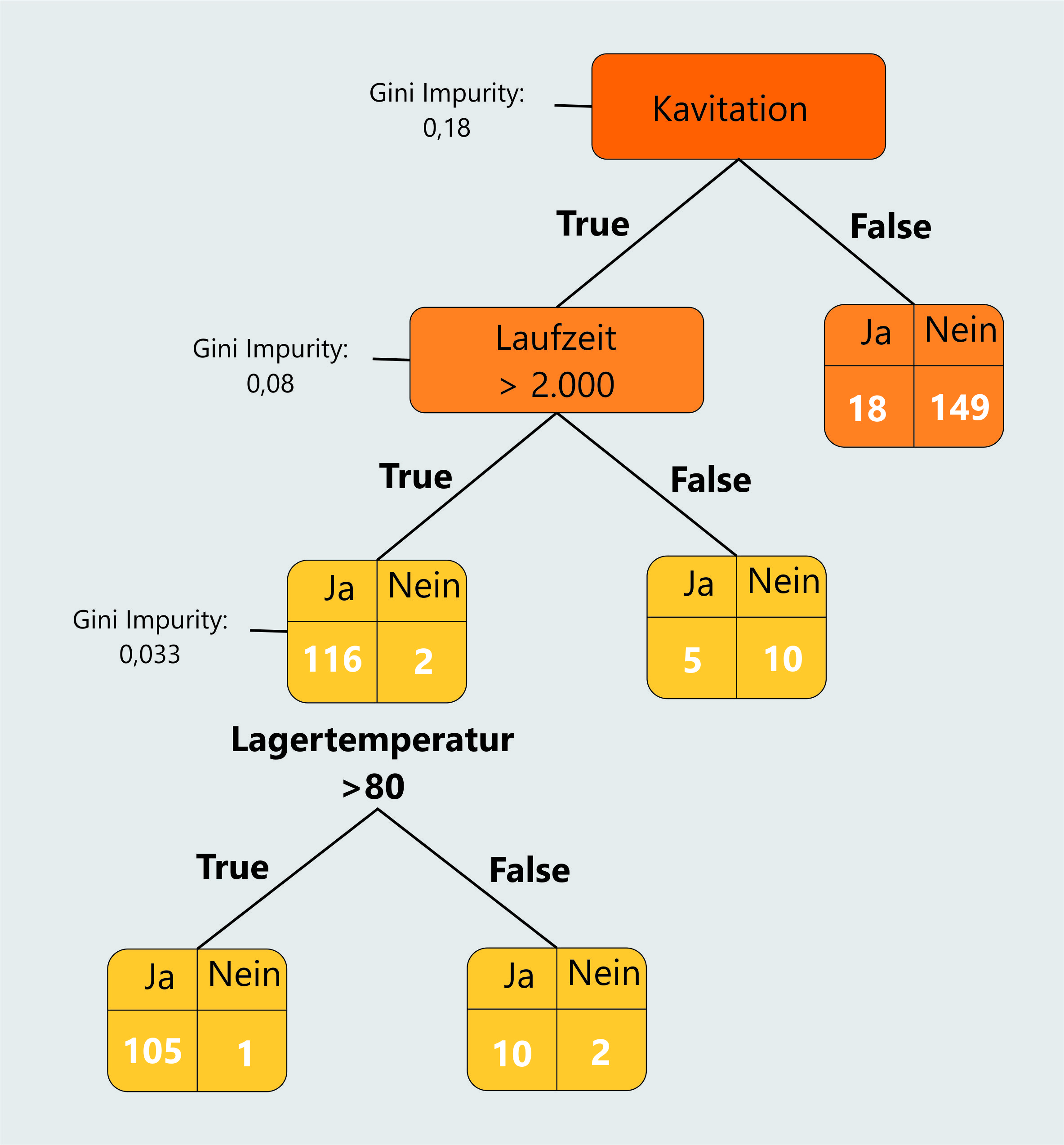
Berechnen wir nun die Gesamt-Impurity mit unseren bekannten Formeln, erhalten wir einen Wert von 0,045. Dieser Wert liegt über unser Impurity von 0,033. Dies bedeutet, dass der Einsatz der Lagertemperatur hier keine Verbesserung der Impurity bewirkt. Aus diesem Grund erfolgt keine weitere Unterteilung nach der Lagertemperatur. Der Knoten Laufzeit True, ist hier also unser Wurzelknoten.
Dieser Teil des Baums besagt, dass von 118 Pumpen die Kavitation und eine Laufzeit größer 2.000 Stunden haben, 116 Pumpen ausfallen. Anders gesagt: Eine Pumpe mit Kavitation und einer so großen Laufzeit fällt zu 98% aus. Wir haben nun diesen Teil des Baumes erfolgreich berechnet. Das gleiche Prozedere müssen wir nun noch für die restlichen Knoten des Baumes machen. Dies führen wir aber nicht mehr im Detail aus. Ein fertiger Baum könnte dann z.B. so aussehen.

Zusammenfassung
Im Betrieb könnte nun für eine neue Pumpe an Hand der drei Parameter Kavitation, Laufzeit und Lagertemperatur in Kombination mit dem erstellten Decision Tree vorhergesagt werden, ob sie ausfallen wird oder nicht. Von dieser Vorhersage können wir dann ableiten, ob die Pumpe gewartet werden sollte oder nicht. Steht ein Ausfall bevor, benötigen wir eine Wartung. Ist ein Ausfall unwahrscheinlich, wird auch keine Wartung benötigt. So können wir das zu Beginn definierte Ziel der zustandsorientierten Instandhaltung umsetzen. Hat eine Pumpe bspw. keine Kavitation und eine Laufzeit kleiner 2.000 Stunden (ganz rechts in der Abbildung) fällt sie mit 98,5 prozentiger Wahrscheinlichkeit nicht aus. Eine Wartung ist also nicht notwendig.
In diesem Beitrag haben wir eine Einführung in den Machine Learning Algorithmus Decision Tree gegeben. Mehrere Decision Trees können zu einem Random Forest verknüpft werden, worauf wir jedoch nicht weiter eingehen. In unserem nächsten Artikel starten wir dann mit künstlichen neuronalen Netzen, mit denen wir uns nun intensiver befassen.


