Der Kern künstlicher neuronaler Netze – Was sich innerhalb eines einzelnen Neurons abspielt
March 7, 2021
7 min
Machine Learning
Nachdem wir uns im letzten Artikel zunächst mit der Notation und dem grundsätzlichen Aufbau von künstlichen neuronalen Netzen befasst haben, können wir uns nun dem Kern der neuronalen Netzen nähern: den Berechnungen. In der folgenden Abbildung ist ein künstliches neuronales Netz dargestellt.

Dieses setzt sich aus drei Layern zusammen: Dem Input Layer, einem Hidden Layer und dem Output Layer. Während der Input Layer nur dazu dient die Daten in das neuronale Netz einzuspeisen, finden im Hidden und Output Layer Berechnungen statt. Die Berechnungen werden innerhalb der einzelnen Neuronen durchgeführt und bilden somit die Basis eines künstlichen neuronalen Netzes. Diesen Berechnungen widmen wir uns in diesem Artikel.
Die Berechnungen innerhalb eines einzelnen Neurons
Wie immer finden wir, dass sich etwas am besten an Hand eines Beispiels erklären lässt. Und ebenfalls wie immer verwenden wir ein Beispiel aus der Pumpenwelt. Wir möchten auf Basis der Leistungsaufnahme und der Drehzahl vorhersagen, ob eine Pumpe ausfällt oder nicht. Damit unser Start jedoch nicht zu kompliziert wird, starten wir mit einem neuronalen Netz ohne Hidden Layer. Dies ist dann zwar kein wirkliches Netz mehr, aber für ein erstes Verständnis besser geeignet. Letztendlich handelt es sich bei unserem Beispiel, um eine logistische Regression, die wir mit einem neuronalen Netz lösen wollen. Wie oben schon beschrieben finden bei einem neuronalen Netz die Berechnungen in den Neuronen des Hidden und Output Layer statt. Wir betrachten nun die Berechnung im Neuron des Output Layers. Diese lässt sich prinzipiell jedoch auch auf die Neuronen des Hidden Layers übertragen. Unser Neuron hat zwei Eingänge, nämlich unsere Werte der beiden Parameter Leistungsaufnahme und Drehzahl. Ziel des Neurons ist es letztendlich einen Zusammenhang zwischen den beiden Paramatern zu erkennen und abzubilden. Die Berechnung innerhalb des Neurons kann in zwei Teile aufgeteilt werden. Den ersten Teil würden wir als linearen Teil bezeichnen, im zweiten Teil wird dann eine sogenannte Aktivierungsfunktion auf diesen linearen Teil angewandt. Als Variablen bezeichnen wir das Ergebnis des linearen Teils als z, den Teil mit der Aktivierungsfunktion als a. Wir berechnen innerhalb des Neurons zunächst z und dann a. Betrachten wir nun den linearen Teil und schauen uns an, was bei einer linearen Funktion abläuft.
Lineare Funktion zur Berechnung von z
Angenommen wir möchten auf Basis der Leistungsaufnahme unserer Pumpe den Förderstrom dieser ermitteln. Anders ausgedrückt, möchten wir auf Basis der unabhängigen Variable (der Leistungsaufnahme), die abhängige Variable (den Förderstrom) bestimmen. Da wir die abhängige Variable nur auf Basis einer anderen Variable bestimmen, spricht man hierbei auch von der einfachen linearen Regression [1]. Um den Zusammenhang zwischen der Leistungsaufnahme und des Förderstroms der Pumpe herauszubekommen, benötigen wir wie immer Daten, dargestellt in der folgenden Abbildung.
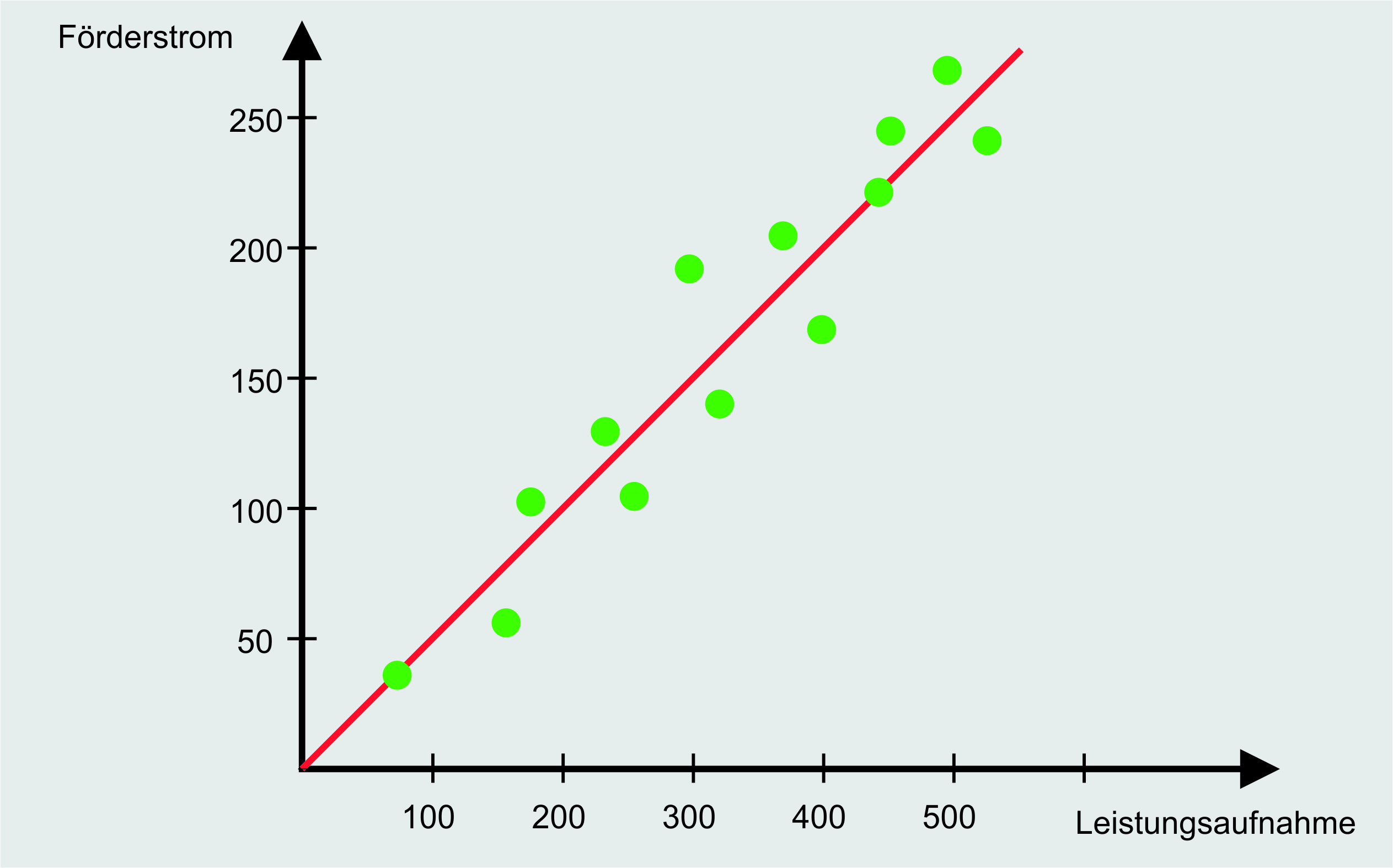
Auf der x-Achse ist die Leistungsaufnahme dargestellt, auf der y-Achse der Förderstrom. Ziel der linearen Regression ist es nun, dass auf Basis der Leistungsaufnahme abgeschätzt werden kann, wie hoch der Förderstrom ist. Die dargestellten Punkte zeigen schon, dass zwischen den aufgenommenen Werten ein linearer Zusammenhang besteht. Dies wird durch die eingezogene Linie verdeutlicht. Um den Zusammenhang der Leistungsaufnahme und des Förderstroms nicht nur graphisch, sondern auch mathematisch herleiten zu können, gibt es wie immer eine Formel, die Regressionsgleichung [2]:
Diese Formel kennen wir auch noch aus der Schule als Geradengleichung, wobei w die Steigung der Geraden und b der Achsenabschnitt auf der y-Achse sind. Ihr werdet hierzu viele andere Bezeichnungen für diese Variablen finden, wir werden im weiteren Verlauf jedoch w und b verwenden. Im Kontext der Regression wird w als Regressionskoeffizient und b als Regressionskonstante bezeichnet. Ziel der linearen Regression ist es nun, die Werte für w und b so zu bestimmen, dass die Korrelation zwischen x und y möglichst genau abgedeckt wird. Wie die Ermittlung der Geraden im Zusammenhang mit künstlichen neuronalen Netzen funktioniert schauen wir uns in weiteren Artikeln genauer an. Im Moment nehmen wir an, dass die optimale Gerade schon bestimmt wurde und w und b die folgenden Werte haben.
Für b wird ein Wert von null bestimmt, da bei keiner Leistungsaufnahme auch kein Förderstrom gefördert werden kann. Leistungsaufnahme und Förderstrom hängen mit dem Faktor zwei zusammen, was durch ein w von 0,5 dargestellt wird. Auf Basis einer gegebenen Leistungsaufnahme kann nun der Förderstrom abgeschätzt werden.
Doch was hat das nun mit der logistischen Regression zu tun? Wie weiter oben beschrieben, möchten wir vorhersagen, ob eine Pumpe ausfällt oder nicht. Wir möchten also eine binäre Klassifikation durchführen. Hierzu verwenden wir die logistische Regression. Bei einer binären Klassifikation kann unser Ausgang nur zwei Werte annehmen: 0 (Ausfall) oder 1 (kein Ausfall). Würden wir nun die lineare Regression verwenden, um den Zusammenhang zwischen der Leistungsaufnahme und dem Ausfall der Pumpe darzustellen, könnten wir Werte rausbekommen, die nicht zwischen null und eins liegen. Dies wird durch das Beispiel der Leistungsaufnahme und des Förderstroms verdeutlicht, da hier Werte für den Förderstrom herauskommen, die jenseits der eins liegen. Wir benötigen also eine Methode, um den ermittelten Wert der linearen Regression auf einen Wert zwischen null und eins zu skalieren. Hier kommt die sogenannte Sigmoidfunktion ins Spiel.
Die Sigmoidfunktion
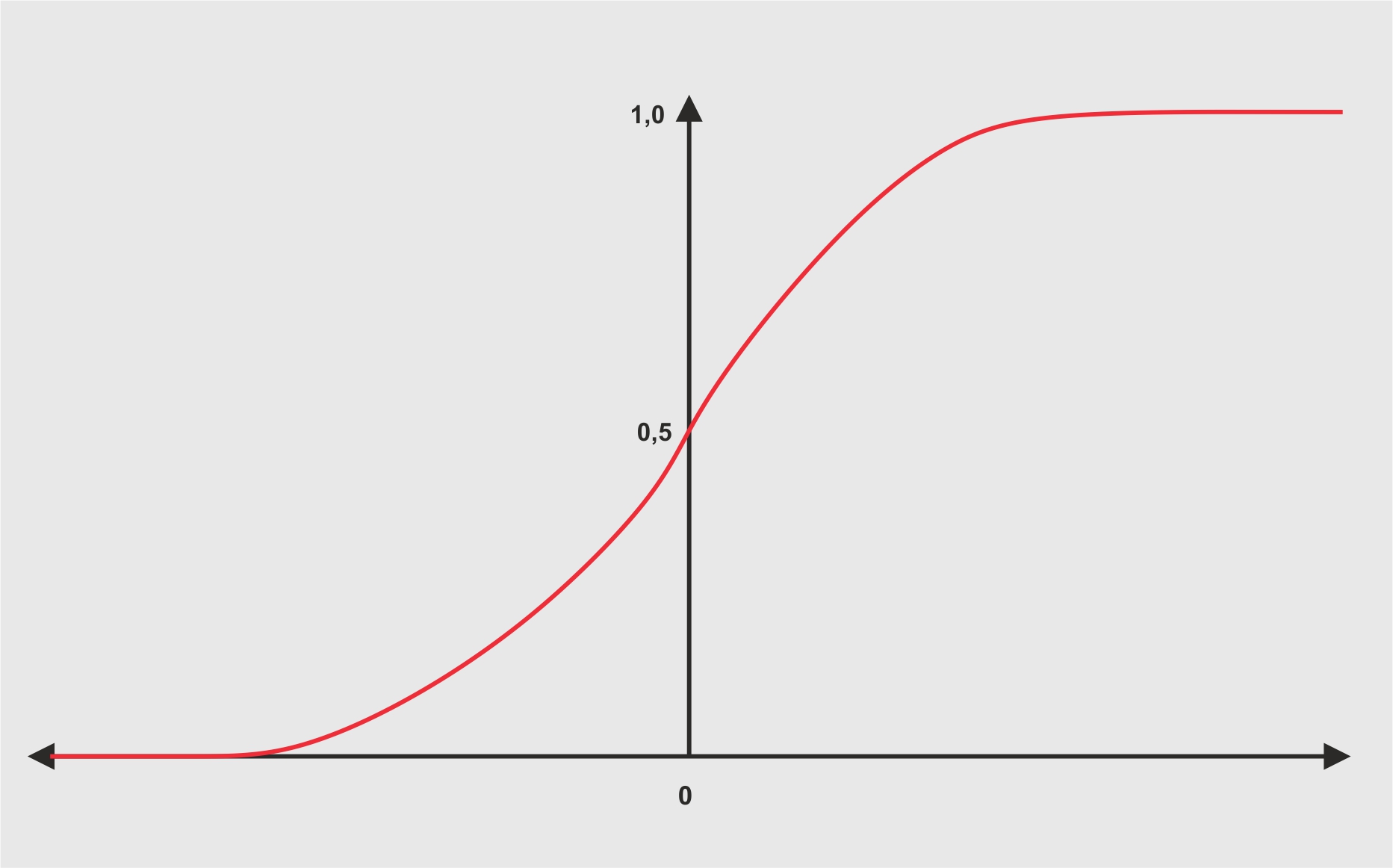
Die Sigmoidfunktion ist eine Aktivierungsfunktion und wird im Bereich der neuronalen Netze häufig verwendet [3]. Die Formel der Sigmoidfunktion sieht folgendermaßen aus.
Das z in der Formel ist unser Ergebnis des linearen Teils. Die Sigmoidfunktion wird eingesetzt, um den linearen Teil auf einen Wert zwischen 0 und 1 zu skalieren. Das dies funktioniert wird deutlich, wenn man die Werte 2, 0 und -2 für z einsetzt.
Die Ergebnisse zeigen vor allem zwei Sachen: Die Skalierung auf einen Wert zwischen 0 und 1 funktioniert, und für positive Zahlen wird ein Wert größer 0,5, für negative Zahlen ein Wert kleiner 0,5 erreicht (Vorzeichen beachten!). Betrachten wir nun den Graphen der Sigmoidfunktion wird dies ebenfalls deutlich.
Wir wissen nun was im linearen Teil des Neurons abläuft und wie auf dieses Ergebnis die Sigmoidfunktion als Aktivierungsfunktion angewendet wird. Wir fassen dies nun für unser Beispiel mit den zwei Parametern der Leistungsaufnahme und Drehzahl zusammen.
Berechnung eines Neurons
Unsere zwei Parameter bezeichnen wir nun als x1 und x2. Bei der linearen Funktion haben wir die beiden Paramater w und b eingeführt. Im Kontext von neuronalen Netzen werden diese als Gewichte bezeichnet. Diese Gewichte sind das was unser neuronales Netz im weiteren Verlauf erlernt. Jedem Parameter wird ein separates w zugeordnet, sodass wir w1 und w2 erhalten. Der Parameter für b wird nur einmal bestimmt. Mit diesen Werten befüllen wir nun unsere Gleichung für z, sodass diese wie folgt aussieht.
Auf das Ergebnis wird die Sigmoidfunktion angewandt, welche uns dann einen Wert zwischen 0 und 1 ausgibt. Zum Abschluss möchten wir mit einem kurzen Beispiel den Ablauf aufzeigen und zu dem nächsten Aspekt hinleiten, den wir im folgenden Artikel betrachten werden. Zu Beginn hatten wir das Ziel definiert, dass unser neuronales Netz erlernen soll den Ausfall von Pumpen vorhersagen zu können. Der Ausfall wurde mit 0 bezeichnet, kein Ausfall entspricht einem Wert von 1. Um die Vorhersagen treffen zu können muss unser Netz entsprechend trainiert werden. Wir betrachten nun ein Trainingsbeispiel und schauen uns an, wie die erste Berechnung in einem untrainierten Netz aussieht. Angenommen wir haben ein Trainingsbeispiel mit Werten von 340 Watt als Leistungsaufnahme und eine Drehzahl von 1.500 Umdrehungen pro Minute. Zusätzlich wissen wir, dass unsere Pumpe ausgefallen ist, also ein y von 0 hat. Zu Beginn des Trainings müssen für unsere Parameter w1, w2 und b Werte eingesetzt werden, da es diese noch nicht erlernt hat. Wie man initial gute Werte einsetzt, schauen wir uns in einem späteren Artikel an, nun setzen wir für jeden Wert 0,5 ein. Mit diesen Parametern können wir zunächst unser z berechnen.
Diesen Wert setzen wir nun in die Formel unserer Sigmoidfunktion ein.
Unser Modell würde also vorhersagen, dass unsere Pumpe ausfällt und sich damit irren, da sie in Wahrheit nicht ausgefallen ist. Nun müssen wir unserem Modell beibringen, dass es seine Parameter anpassen muss, um bessere Vorhersagen zu machen. Der erste Schritt hierzu ist den sogenannten Verlust zu bestimmen. Was dieser Verlust ist und wie er berechnet wird, schauen wir uns im nächsten Artikel an.


